Cracking The Coding Interview Together – Problem 2.8: Loop Detection

Today’s problem is one that almost every serious interview prep book includes—and for good reason. On the surface, it sounds simple: detect a loop in a linked list. But the real challenge isn’t detecting the loop; it’s identifying where the loop begins.

This problem is less about syntax and more about understanding how pointers move, how cycles behave, and how to explain your thinking clearly to an interviewer. So let’s slow down and do this the right way.

As always, we’ll follow the same structure that you would use in a real interview.

1. Understand the problem statement together
2. Ask any questions, that you would like to ask the interviewer
3. I would urge you to take your time here and try to come up with your own solution before going forward
4. Think how you would go about solving the problem(you would be talking out loud in front of the actual interviewer)
5. Write code and understand how it works and explain it to your interviewer

Problem statement

Loop Detection
Given a circular linked list, implement an algorithm that returns the node at the beginning of the loop.

And a clarification is provided:

Circular linked list: A (corrupt) linked list in which a node’s next pointer points to an earlier node, forming a loop.

Analyse the problem statement together

Example

A → B → C → D → E
          ↑     ↓
          └─────┘

Input

A → B → C → D → E → C

Output

c

The important detail here is subtle but critical:
The loop does not start at the head of the list. It can start anywhere.

Also notice that the output is the node itself, not its value, not its index—the actual node reference.

Questions for the interviewer

Before writing any code, this is the point where you pause and clarify assumptions. Interviewers expect this.

Here are the questions I would ask:

1. Can the linked list be empty?
2. Can the list contain only one node?
3. Is there guaranteed to be a loop, or could there be none?
4. If there is no loop, should we return null?
5. Is the list singly linked?

Typical answers would be:

• Yes, the list can be empty
• Yes, it can have one node
• No, a loop is not guaranteed
• Return null if no loop exists
• Yes, it is a singly linked list

These answers shape the solution more than people realize.

Think about the Solution

This is important.

Before reading further, stop for a minute and ask yourself:

• How would I detect a loop?
• Once I know there is a loop, how would I find where it starts?
• What information can I use without modifying the list?

If you’ve heard of Floyd’s Cycle Detection Algorithm, you might already have ideas forming. If not, that’s perfectly fine—this post is meant to build that intuition from scratch.

Think Out Loud: How Would You Approach This?

Let’s reason step by step, just like you would while speaking to an interviewer.

First Thought: How do I even know there is a loop?

A linked list normally ends with a null pointer.
If there is a loop, you’ll never hit null.

One common technique is to use two pointers:

• One moves slowly (one step at a time)
• One moves fast (two steps at a time)

If there is a loop, the fast pointer will eventually catch up to the slow one.

This gives us loop detection.

But the real question is:

Once they meet, how do we find the start of the loop?

This is where the problem becomes interesting.

The Intuition Behind the Solution

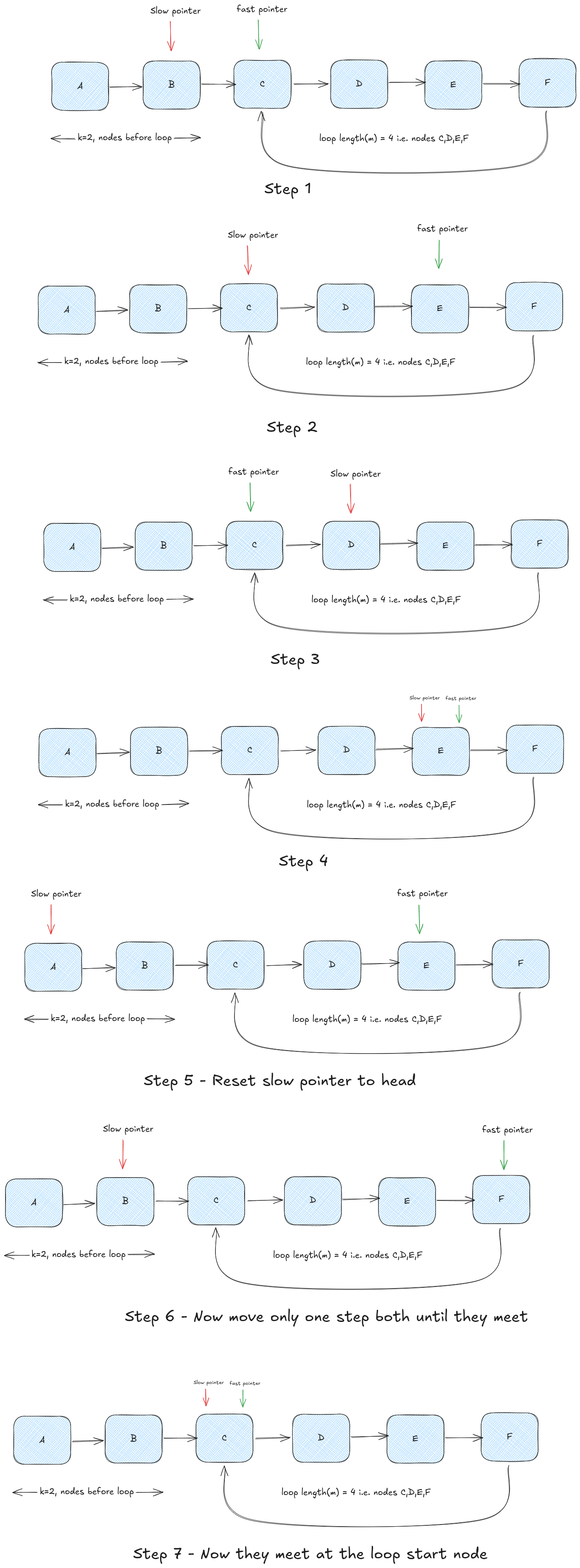
Let’s introduce some notation:

• Let k be the number of nodes before the loop starts
• Let m be the length of the loop

When the slow and fast pointers meet:

• The slow pointer has traveled k + x steps
• The fast pointer has traveled 2(k + x) steps

The difference in distance must be a multiple of the loop length:

2(k + x) − (k + x) = k + x = m

This leads to a powerful insight:

If you place one pointer at the head and keep the other at the meeting point, then move both one step at a time, they will meet exactly at the start of the loop.

This is not magic. It’s math and pointer alignment.

Write code and explain

Now let’s translate this idea into code.

Java code

Node Definition (Assumed)

class ListNode {
    int value;
    ListNode next;

    ListNode(int value) {
        this.value = value;
        this.next = null;
    }
}

Detect the loop

public static ListNode detectLoop(ListNode head) {
    if (head == null || head.next == null) {
        return null;
    }

    ListNode slow = head;
    ListNode fast = head;

    // First phase: detect if a loop exists
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;

        if (slow == fast) {
            break;
        }
    }

    // No loop found
    if (fast == null || fast.next == null) {
        return null;
    }

    // Second phase: find start of loop
    slow = head;
    while (slow != fast) {
        slow = slow.next;
        fast = fast.next;
    }

    return slow;
}

Here’s how I would explain this to an interviewer:

1. I use two pointers, slow and fast, to detect whether a loop exists.
2. If they never meet, the list is not circular.
3. Once they meet, I reset one pointer to the head.
4. I then move both pointers one step at a time.
5. The node where they meet again is the start of the loop.

Simple, calm, and confident.

Time & Space Complexity

Let’s be explicit — interviewers care about this.

• Time Complexity: O(n)
  Each pointer traverses the list at most a constant number of times.
• Space Complexity: O(1)
  No extra data structures are used.

Final Thoughts

This problem is a great reminder that interviews are not about memorizing tricks. They are about reasoning, communication, and clarity of thought.

If you can explain this solution clearly—especially the intuition behind why resetting the pointer works—you are demonstrating exactly what interviewers are looking for.

Take your time with this one. Draw it out on paper. Walk through the pointers step by step. Try explaining it aloud.

That’s how these concepts truly stick.

I’ll see you in the next one. Until then—happy coding.